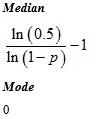PsiGeometric (p,...)
PsiGeometric (p) is a discrete distribution of the number of failures before the first success in a sequence of independent ‘Bernoulli Trials’ (experiments with exactly two possible outcomes), where p is the success probability in each trial. The Geometric distribution can be used to model the number of losing trades before the first winning trade, the number of items passing inspection before the first defective item appears in a batch, etc.
PsiGeometric (p) can be considered as a discrete analog of the (continuous) Exponential distribution. If X1, X2, …, Xn are independent geometrically distributed random variables with parameters p1, p2, …,pn, then X = min (X1, X2, …, Xn) is also a Geometrically distributed random variable with parameter p = 1 – [(1-p1)(1-p2)…(1-pn)]. Additionally, if X1, X2, …, Xn are Geometrically distributed random variables with parameter p, then their sum is Negative Binomially distributed with parameters n, p.